Deflation-based Krylov subspace method:
Developing an interactive simulation environment for electrosurgery that includes coupled electro-thermo-mechanical multiphysics modeling, continuum level, micromechanical level multilevel modeling and topological change can be challenging. Current best practices for the efficient solution of such problem are based almost exclusively on multigrid methods and preconditioned Krylov subspace methods. Design of efficient application specific monolithic multiphysics multigrid solvers or preconditioners is challenging. Therefore, our aim in this project is to develop efficient finite element solver and block preconditioning technique that can effectively deflate the spectrum of the system matrix leading to exponential convergence of the Arnoldi iterations for the multiphysics, multilevel modeling of electrosurgery without compromising physical fidelity and stability. Research efforts are focused on:
- Deflation based block preconditioner for efficient solution of electrosurgical simulation
- Reduced order modeling of large scale electrosurgical simulation
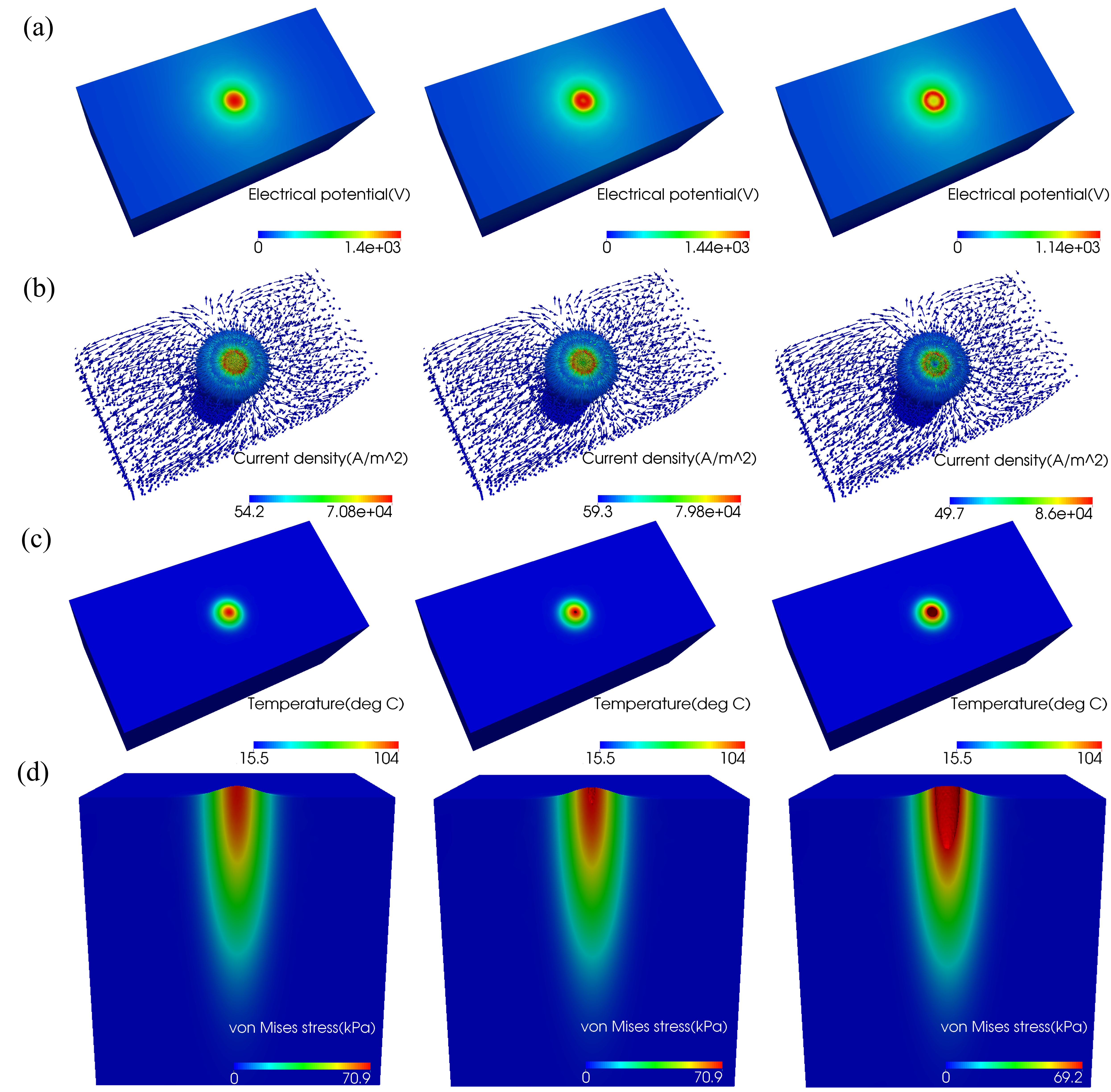
Contour plots for 50 W power setting with a fixed active electrode
Multigrid method:
Multilevel cutting is complicated by the need to reflect fine grid topology changes at the coarser grid level which requires modification of the coarse grid operators. We consider a two-level formulation and address the real time issue by developing two separate strategies for updating the map relating the coarse and fine grid operators for structured as well as unstructured meshes. Considerable speedups of this ultigrid approach compared to a preconditioned conjugate gradient (PCG) solver are observed.

Algorithms for cutting of deformable objects simulated using multilevel methods
Acceleration using Convolutional networks
- Investigating the possibility of using convolutional networks to reduce the computational complexity of large scale multiphysics simulation in electrosurgery
- Performing data-augmentation to the input pressure fields without the need of running exact solvers
- Creating a set of geometry using level set evolution with randomized velocity for generalization performance with topological change
